写到最初
对于一个程序,他总是要经历预处理–编译–链接三个步骤,其中编译是非常重要的一步,他成功搭起了从高级语言到二进制指令集的桥梁,从此程序员得以解脱繁杂的机器语言乃至汇编的桎梏专心于高级语言的开发。
1.理论框架
词法分析的根本作用在于读取源程序组成词素进而产生词法单元(token) ,再得到语法单元之后对它们再做语法分析等后续处理。
1.1 词法单元(token)
词法单元是一个结构体 ,由一个词法单元名 和属性值 组成,词法单元名表示词语的种类,而属性值则表征该词语的具体内容。故属性值对于变量以及字符串可以作为指针 ,数字和运算符则取对应的具体数字或具体运算符。token的结构可以如下:
1 2 3 4 5 6 7 8 typedef struct token { char *token_name; union { int num; char op; char *p; } }Token;
但是为了实验的方便我们可以选择简化方案,既然词法单元名是用于分类那么我们完全可以采用整数形式代替,比如种别码 。而对应单元的属性值则用字符串代替,就表示为该单词的字符串值。于是结构改写为:
1 2 3 4 typedef struct token { int TYPE_CODE; char name[32 ]; }Token;
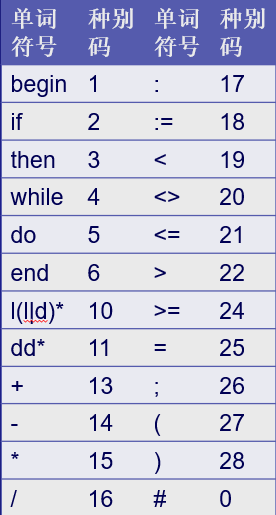
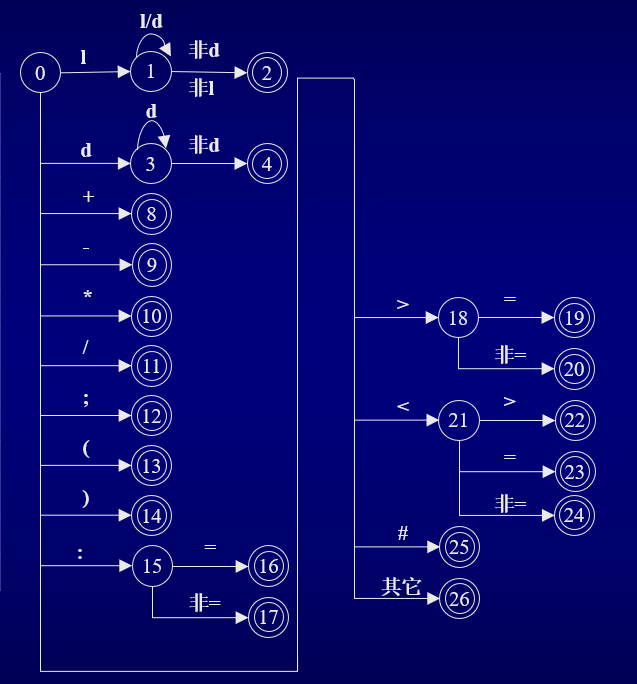
不妨假设种别码:
于是有例子,对句子:begin x:= 3; if x>0 then x:=x+3*2 ; end # 在按照上述结构规则经过词法分析器扫描后产生的tokens为(1,begin) (10,x) (18,:=) (26,;) (2,if) (10,x) (22,>) (11,0) (3,then) (10,x) (18,:=) (10,x) (13,+) (11,3) (15,*) (11,2) (26,;) (6,end) (0,#) ,后续我们也可以用代码来实现同样的结果,值得注意的是这里“then”,“:=”均为字符串。不过在考虑代码之前我们先得清楚编程背后的思想:文法 和自动机 。
1.2 有穷自动机(finite automation,FA)
1.2.1 程序是一个自动机
谈及到程序 本身时我们往往会联想到代码 ,即在编辑器上所写的一行行文字信息,但这只是一种静态 的思维。而当程序一旦运行起来之后,他便开始按照顺序(或者并发)规则开始工作,经历若干分支或循环结构计算出需要的数值。把这个过程高度抽象来看会发现其实程序本质 就是按照一定的时间间隔通过某个转移条件从一个状态转移到另一个状态 ,即状态转移的自动机 。换句话来说,任何程序原则上都可以转化为一个自动机,同样一个自动机也可以转化为某个程序。不光程序如此CPU本质上也可以理解为一个自动机 ,在南大蒋炎岩老师的操作系统 中也特别强调了该点。
1.2.2 有穷自动机
对一个自动机而言如果存在有限个 状态同时存在终结态 则可以称为有穷自动机 。状态之间存在转移条件边,可以将自动机视为有向图 。它的结构可以通过五元组描述:’ M = ( Q , Σ , f , S , Z ) M=(Q,\Sigma,f,S,Z) M = ( Q , Σ , f , S , Z ) Q Q Q 状态集 ,’Σ \Sigma Σ 输入字母表 ,即状态之间的转移条件集合, f f f Q × Σ Q\times\Sigma Q × Σ Q Q Q S S S 初态 (注意它是唯一的 ), Z Z Z
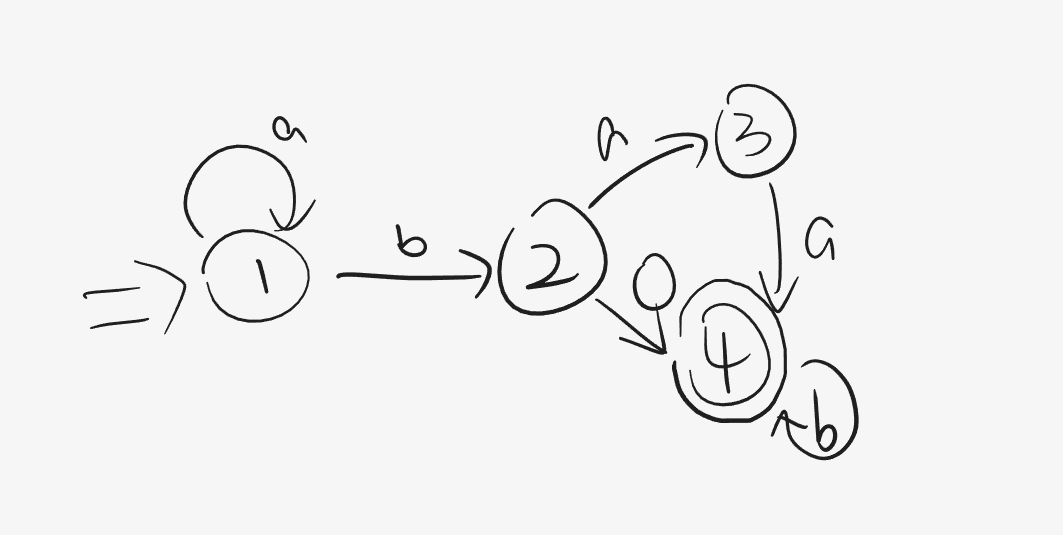
例如:
其中1、2、3、4均为状态,而方向箭头表示条件转移。这里拿初始状态 1举例便是遇到条件a则继续重复状态1,否则若遇到b则转移到状态2中。特别的,对于状态4通过两个圆表示它是一个终结态 。那么一个空串 (可以理解为空集合,由于编译原理主要面向字符串 ,所以主要对象就是集合 和集合元素组成的串 )从1状态出发后经过条件b和条件0达到终态4,所形成的串便是b0,也可能经过a、b、a、a形成abaa。
该例子对应的五元组: M = ( Q = { 1 , 2 , 3 , 4 } , Σ = { a , b , 0 } , f , S = 1 , Z = { 4 } ) M=(Q=\{1,2,3,4\},\Sigma=\{a,b,0\},f,S=1,Z=\{4\}) M = ( Q = { 1 , 2 , 3 , 4 } , Σ = { a , b , 0 } , f , S = 1 , Z = { 4 } ) f ( 1 , a ) = 1 , f ( 1 , b ) = 2 , f ( 2 , a ) = 3... f(1,a)=1,f(1,b)=2,f(2,a)=3... f ( 1 , a ) = 1 , f ( 1 , b ) = 2 , f ( 2 , a ) = 3 . . .
那么反过来给你一个字符串α \alpha α 推理 它是否成立,比如这里如果 α = a a b b \alpha=aabb α = a a b b 按照前三个字符到了状态2而第四个字符b是一个状态2所没有的转移条件,于是 α \alpha α ,或者说他的词法错误。更一般的,用我们常听到的话来讲:它无法通过编译 。
由此我们就对有穷自动机有了初步的印象:有了他我们便可以按部就班的编写程序来做词语的推理。(编译器怎么知道for是特殊的?它怎么区分begins和begin?看到这里聪明的你应该明白了自动机的重要性)
1.2.3 分类:
DFA (确定有穷自动机):转移条件f是单值映射 ;(一对一,一个条件确定一个状态)NFA (非确定有穷自动机):f是多值映射 ;(一对多 ,所谓某个条件可以转移到多个状态,即非确定 的)
其中最重要的便是DFA。对于顺序结构的程序而言它总存在一个唯一 的最小DFA ,如果我们按照需求得到对应的DFA便可以非常容易的写出代码,词法分析器也不例外。我们的目标便是将词法规则 转化为对应的那个DFA。于是问题来了:
词法规则如何变成DFA呢?答曰:正规文法 。
1.3 文法:推理句子的法则
当我们确定一个单词在代码合不合法时是按照语法,或者严格意义来说是按照词法 来确定的。比如cout在c++中不会报错,但在C中如果没有相关定义声明就无法通过编译;同样的,你在C语言中输入if即使没有声明这个变量编译也能通过,不光能够通过编译而且还能识别出这是一个特殊符号:表示条件分支。
词法在下文我们统称为文法 ,它的结构是一个四元组 ,即文法M表示为 M = ( V N , V T , S , P ) M=(V_N,V_T,S,P) M = ( V N , V T , S , P ) V N :非终结符号集 , V T : 终结符号集 , P : 规则集 , S : 起始符号 V_N:非终结符号集,V_T:终结符号集,P:规则集,S:起始符号 V N : 非 终 结 符 号 集 , V T : 终 结 符 号 集 , P : 规 则 集 , S : 起 始 符 号 ->表示产生,比如A->a就被称为一条产生式 ,也称为一条规则。产生式左部 就是非终结符 ,而右部不可再推 的字符串元素就被称为终结符 。其中 ϵ \epsilon ϵ 空串 长度为0,可以认为字符串 α ϵ β \alpha\epsilon\beta α ϵ β α β \alpha\beta α β α \alpha α β \beta β
文法另一种常见的写法便是:
1 2 3 4 G[S]: S->aA|bB A->a|aA B->b|bB
在这种写法下我们也可以很快得到该文法G的信息,S为起始符,三个产生式为规则集P P P 或 ,属于BNF 的用法,具体可见巴科斯范式(BNF) 。
有了文法我们就可以十分方便推出单词格式了,上文中G[S]进行几步推理易得出单词(也称为句子 )格式: a a . . . aa... a a . . . b b . . . bb... b b . . . 语言 ,用 L ( G [ S ] ) L(G[S]) L ( G [ S ] )
1.3.1 正规文法
文法分为四种 ,0/1/2/3型文法。详细名称:(epsilon== ϵ \epsilon ϵ
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 //0型文法:无限制文法,即该文法无特殊约束 (图灵机采用的文法 S->0AB 1B->0 B->SA|01 ... //1型文法:上下文有关文法,即产生式左部可能存在终结符 S->0AB 0A->C ... //2型文法:上下文无关文法,即产生式左部不存在终结符 S->0AB A->C B->1C|D ... //3型文法:正规文法,在上下文无关文法的基础上有约束:A->aA|a或者A->Aa|a(a可以属于epsilon) S->0A A->B B->1C
如此可见,越往下文法的规则越严格,范围自然也就越小。而我们需要的便是其中最严格的正规文法 ,已经证明正规文法是一定可以写出该文法对应的DFA。
注意1:一般正规文法最好采取右线性文法,即A->cA|c的格式,左线性文法(A->Ac|c)会出现左递归现象,需要后续花时间消除。
那么总结下来,当我们为一种文法规则写词法分析器时我们可以采用以下流程管道:
P:正规文法—>得到NFA—>转化为DFA—>DFA最小化—>利用DFA实现代码
注意2:由于起点不同你也可以不考虑此流程,比如起点是正规式而非正规文法,或者你已知DFA等等,流程不唯一,这里采取的是比较规范标准的一种流程。
那么接下来我们就从流程管道P的每一个步骤开始,一步步实现词法分析器。
2.流程管道
2.1 从文法到状态转移图
这其中有两部分内容:正规 文法–>NFA与NFA–>DFA,其中正规文法到NFA比较简单故将两部分合在一块。
2.1.1 画NFA
对文法的每一条产生式都写成一条映射函数,比如A->aB可以写为: f ( A , B ) = a f(A,B)=a f ( A , B ) = a
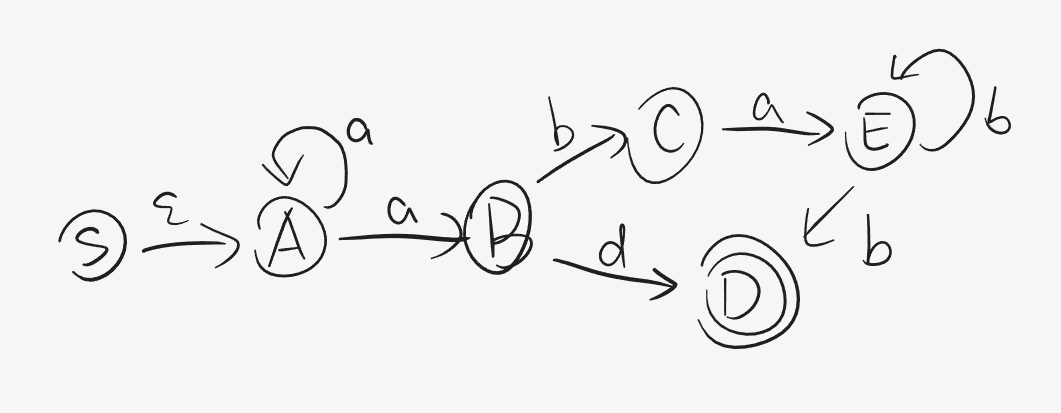
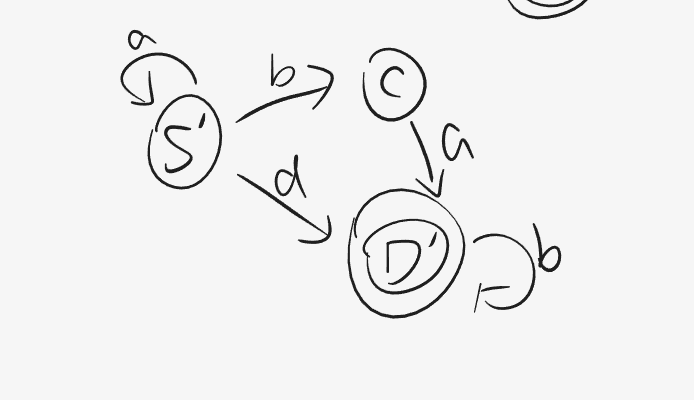
假设存在文法:
1 2 3 4 5 6 7 G[S]: S->A(也就是S->epsilonA) A->aB|aA B->bC|dD C->aE D->epsilon E->bE|bD
我们可以得到初步的状态转移图:
显然我们可以发现存在多值映射,比如 f ( A , a ) = { A , B } f(A,a)=\{A,B\} f ( A , a ) = { A , B }
2.1.2 一一对应的DFA
拥有NFA后我们便要考虑NFA的确定化,即对任意的 NFA都有对应的DFA使他们接受相同的 语言。DFA的好处就是他的映射是单值 的,对一个非终结符A我们读取到下一个字符a便能确定唯一的 下个状态B(终结符或 非终结符)这样才方便我们词法分析代码的编写。
2.1.2.1 规则
核心理念:DFA的每一个状态表示NFA的一部分状态集合。
转化过程中主要问题有两点:多值和 ϵ \epsilon ϵ
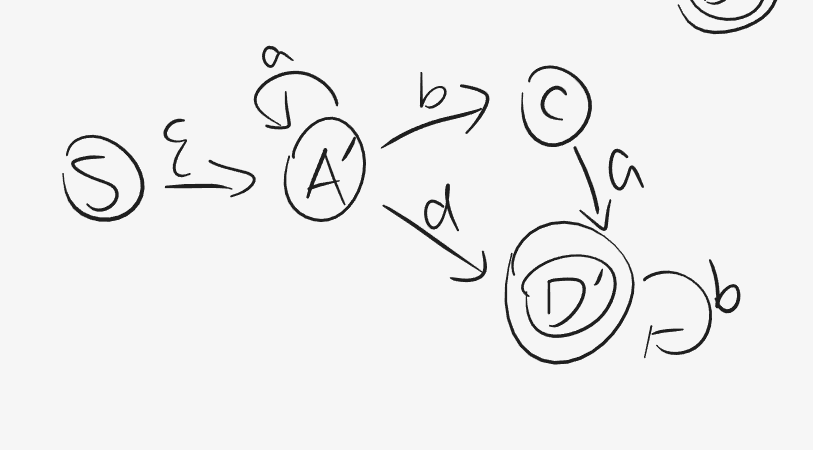
关于多值 ,我们观察上文中的2_1例子,这里从状态 A对条件a有两个选择A/B,也就是多值情况,于是我们考虑将A、B作为一个集合A’。同理有E、D作为一个集合D‘。那么改写完后的NFA为:
除了多值以外的问题,NFA还有一种常见的问题: ϵ \epsilon ϵ ϵ \epsilon ϵ S − > ϵ A < = > S − > A S->\epsilon A<=>S->A S − > ϵ A < = > S − > A ϵ − 闭包 \epsilon-闭包 ϵ − 闭 包 ϵ − C L O S U R E ( I ) \epsilon-CLOSURE(I) ϵ − C L O S U R E ( I )
2.1.2.2 ϵ − C L O S U R E ( I ) \epsilon-CLOSURE(I) ϵ − C L O S U R E ( I )
ϵ − C L O S U R E ( I ) \epsilon-CLOSURE(I) ϵ − C L O S U R E ( I ) 集合 I经过若干次 ϵ \epsilon ϵ 集合 。按照概念对状态 s s s
若 s ∈ I , 则 s ∈ ϵ − C L O S U R E ( I ) 若s\in I,则s\in \epsilon-CLOSURE(I) 若 s ∈ I , 则 s ∈ ϵ − C L O S U R E ( I )
若 s ∈ I , 那么从 s 出发经过任意条 ϵ 弧的任何状态 s ′ ,都属于 ϵ − C L O S U R E ( I ) 若s\in I,那么从s出发经过任意条\epsilon弧的任何状态s',都属于\epsilon-CLOSURE(I) 若 s ∈ I , 那 么 从 s 出 发 经 过 任 意 条 ϵ 弧 的 任 何 状 态 s ′ , 都 属 于 ϵ − C L O S U R E ( I )
得到的闭包即可作为新的状态替代原来的状态集合,对上图而言: S , A ∈ ϵ − C L O S U R E ( S ) S,A\in \epsilon-CLOSURE(S) S , A ∈ ϵ − C L O S U R E ( S ) S ′ = { S , A } S'=\{S,A\} S ′ = { S , A } S ′ S' S ′
实际上由于这个DFA是一个最简DFA ,因此得到它后就可以按照他的逻辑写该文法对应的词法分析器代码了,但是考虑到一般情况我们可能会在得到DFA后发现这个自动机存在冗余状态 ,因此还需要一步:DFA的化简。
2.2 简化的追求
简化DFA的原则是将冗余的状态们组成一个集合视为一个状态。核心理念为:如果一个子集所有状态对已有条件只会转移到自身集合或者全部转移到外部,那么这个集合就可以化简为一个状态。
我们先来看算法:
1 2 3 4 5 6 7 1对DFA状态集Q划分为两个子集:终态集E和非终态集F,划分命名为Gamma=(F,E) 2考虑Gamma每一个集合F中产生式所有的转移条件,对它们进行遍历 2.1根据F的产生式们,对转移条件x推出对应的状态集合H 2.2判断H是否只在F中或是只在Gamma中的其他某个集合Ei中 2.2.1如果不是,即H同时含有F和Ei中的状态,那么在F中找出这些状态集合A,剔除后使得剩余状态对转移条件x推出的状态集仅在F中,而集合A成为划分Gamma的新元素。即新划分Gamma'=(F',A,E1',E2',E3'...,Ei',...) 2.2.2如果是,那么划分不改变,即Gamma'=Gamma 3如果Gamma'=Gamma,算法结束。反之重复步骤2
如果算法看不懂,那我们就引入书上看过的一个例子
首先按照算法,由于 E E E γ = ( F , E 1 ) \gamma=(F,E_1) γ = ( F , E 1 ) F = { A , B , C , D } , E 1 = { E } F=\{A,B,C,D\},E_1=\{E\} F = { A , B , C , D } , E 1 = { E } E 1 E_1 E 1 F a F_a F a F b F_b F b Σ = { a , b } \Sigma=\{a,b\} Σ = { a , b } F a = { A , B } F_a=\{A,B\} F a = { A , B } F b = { C , D , E } F_b=\{C,D,E\} F b = { C , D , E } F b F_b F b F , E 1 F,E_1 F , E 1 F F F F b F_b F b E E E D D D D->bE,因此将 F F F F ′ = { A , B , C } F'=\{A,B,C\} F ′ = { A , B , C } E 2 = { D } E_2=\{D\} E 2 = { D } γ ′ = ( F ′ , E 1 , E 2 ) \gamma'=(F',E_1,E_2) γ ′ = ( F ′ , E 1 , E 2 ) γ ≠ γ ′ \gamma\neq\gamma' γ = γ ′ γ ’ \gamma’ γ ’
同上文, E 1 , E 2 E_1,E_2 E 1 , E 2 F ′ = { A , B , C } F'=\{A,B,C\} F ′ = { A , B , C } F ’ b = { C , D } F’_b=\{C,D\} F ’ b = { C , D } F ′ , E 2 F',E_2 F ′ , E 2 F ′ F' F ′ B B B E 3 E_3 E 3 γ ′ ′ = { F ′ ′ , E 1 , E 2 , E 3 } \gamma''=\{F'',E_1,E_2,E_3\} γ ′ ′ = { F ′ ′ , E 1 , E 2 , E 3 } γ ′ ′ \gamma'' γ ′ ′ F a ′ ′ = { B } ⊂ E 3 F''_a=\{B\}\subset\ E_3 F a ′ ′ = { B } ⊂ E 3 F b ′ ′ = { C } ⊂ F ′ ′ F''_b=\{C\}\subset F'' F b ′ ′ = { C } ⊂ F ′ ′ γ ′ ′ \gamma'' γ ′ ′ γ ′ ′ ′ = γ ′ ′ \gamma'''=\gamma'' γ ′ ′ ′ = γ ′ ′ F ′ ′ F'' F ′ ′ A , C {A,C} A , C A ′ A' A ′
新的DFA则是最小DFA,它含有4个状态。到此,我们终于得到了最小的有穷自动机,接下来就可以按照该DFA的流程写代码了。
3.代码时间
经历了这些理论的洗礼之后终于可以开始实践啦,我们把目光重新聚焦到实际问题上去:如何识别一个特殊单词?
3.1 if,fi,1f的区别
这三个词显然if是特殊单词表示分支结构,fi是一个普通单词可能表示一个变量,1f是一个非法单词无法通过编译。我们对它们的区分正是源于语法规则,一个单词如果第一个字是数字,那么它要么是数字要么是非法单词。如果一个单词第一个字是字母,那么便可以确定它一定是一个由字母组成的“单词”,继而再判断它是关键字还是普通变量。
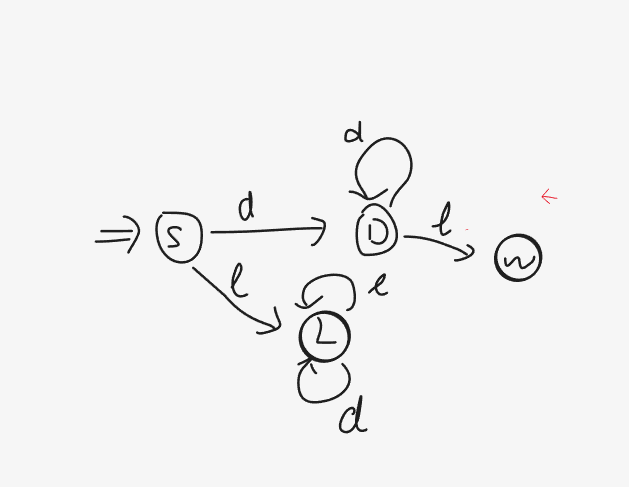
也就是说上述内容很容易转换为一个DNF,它由初状态空串S开始,如果遇到的第一个字符是数字 ( d ) (d) ( d ) ( l ) (l) ( l )
其中状态L定义为文本单元 ,它由一个字符开头后续由字符或者数字组成,于是它在编程语言中可以表示关键字 (如if,switch)或者普通变量 (如a2,ptr1)。而状态D定义为数字单元 ,它完全由数字组成,如果此时检索到了一个字符l l l 词法错误 。
那么此时我们便可以区分出if,fi,1f了:if和fi送入状态L等待后续的再区分,而1f由于首位是数字则送入D,而第二位又是个字符于是送入到状态W产生报错信息。
3.2 DNF总图
除了确定关键字、数字以及普通变量外我们还需要确定运算符等符号,于是类似上文可以得到一张完整的DNF图:
3.3 回到起点
还记得最初的那张种别码的图片吗
我们接下来的想法就是以此图为参照按照总图的结构识别出每一个词法单元并赋予属性值。于是有代码(词法扫描部分):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 char getch (FILE *p) char getbc (FILE *p) bool letter (char ch) bool digit (char ch) void concat (char ch, char *token) int reserve (char *token) void retract (FILE *p) void retractn (FILE *p, int n) char * dtb (char *token) Token scaner (FILE *read) { Token word; char token[30 ]; token[0 ]='\0' ; char ch; ch=getbc(read); if (letter(ch)){ while (letter(ch)||digit(ch)){ concat(ch,token); ch=getch(read); } retract(read); int c=reserve(token); word.TOKEN_TYPE=c; strncpy (word.data.words,token,strlen (token)+1 ); return word; } else if (digit(ch)){ while (digit(ch)){ concat(ch,token); ch=getch(read); } retract(read); word.TOKEN_TYPE=11 ; char * bits=dtb(token); strncpy (word.data.words,bits,strlen (bits)+1 ); return word; } else { switch (ch){ case '+' : word.TOKEN_TYPE=13 ;strcpy (word.data.words,"+" ); return word; break ; case '-' : word.TOKEN_TYPE=14 ;strcpy (word.data.words,"-" ); return word; break ; case '*' : word.TOKEN_TYPE=15 ;strcpy (word.data.words,"*" ); return word; break ; case '/' : word.TOKEN_TYPE=16 ;strcpy (word.data.words,"/" ); return word; break ; case ';' : word.TOKEN_TYPE=26 ;strcpy (word.data.words,";" ); return word; break ; case '(' : word.TOKEN_TYPE=27 ;strcpy (word.data.words,"(" ); return word; break ; case ')' : word.TOKEN_TYPE=28 ;strcpy (word.data.words,")" ); return word; break ; case '#' : word.TOKEN_TYPE=0 ;strcpy (word.data.words,"#" ); return word; break ; case '=' : word.TOKEN_TYPE=25 ;strcpy (word.data.words,"=" ); return word; break ; case ':' : ch=getch(read); if (ch=='=' ){ word.TOKEN_TYPE=18 ;strcpy (word.data.words,":=" ); return word; } else { word.TOKEN_TYPE=17 ;strcpy (word.data.words,":" ); return word; retract(read); } break ; case '<' : ch=getch(read); if (ch=='>' ){ word.TOKEN_TYPE=20 ;strcpy (word.data.words,"<>" ); return word; } else if (ch='=' ){ word.TOKEN_TYPE=21 ;strcpy (word.data.words,"<=" );return word; } else { word.TOKEN_TYPE=19 ;strcpy (word.data.words,"<" ); return word; retract(read); } break ; case '>' : ch=getch(read); if (ch=='=' ){ word.TOKEN_TYPE=24 ;strcpy (word.data.words,">=" ); return word; } else { word.TOKEN_TYPE=22 ;strcpy (word.data.words,">" ); return word; retract(read); } break ; } } } void retract (FILE *read) fseek(read,-1 ,SEEK_CUR); } char getch (FILE *read) return (char )fgetc(read); } char getbc (FILE *read) char ch; ch=getch(read); while (ch==' ' ){ ch=getch(read); } return ch; } bool letter (char ch) if ('a' <=ch&&ch<='z' ||'A' <=ch&&ch<='Z' ){ return true ; } else return false ; } bool digit (char ch) if ('0' <=ch&&ch<='9' ){ return true ; } else return false ; } void concat (char ch, char *token) int i=0 ; while (token[i]!='\0' ){ i++; } token[i]=ch; token[i+1 ]='\0' ; } int reserve (char *token) if (strcmp (token,"begin" )==0 ) return 1 ; else if (strcmp (token,"if" )==0 ) return 2 ; else if (strcmp (token,"then" )==0 ) return 3 ; else if (strcmp (token,"while" )==0 ) return 4 ; else if (strcmp (token,"do" )==0 ) return 5 ; else if (strcmp (token,"end" )==0 ) return 6 ; else return 10 ; } char * dtb (char *token) return token; } void retractn (FILE *p, int n) for (int i=0 ;i<n;i++){ retract(p); } }
我们带入到文本文件a中
1 2 begin x:=9 ; x:=2 *3 ; b:=a+x end #
最后得到的结果便得到一组token结果:
1 (1,begin)(10,x)(18,:=)(11,9)(26,;)(10,x)(18,:=)(11,2)(15,*)(11,3)(26,;)(10,b)(18,:=)(10,a)(13,+)(10,x)(6,end)(0,#)(0,#)
尾巴
写到这里词法分析部分 就终于完成了,有了token后我们便会开始想如何确定词法单元无误的情况下如何确定一条语句 是否有语法错误 呢?这就是后续的语法分析 问题了。